YawPitchRollCalculation

This document describes how the orientation of the IMU in terms of yaw,pitch, and roll is calculated from the information provided by the IMU (we use the MPU-9250).

1 Calculations as done on the Arduino

The result of the calculations in the Digital Motion Processor (DMP) done in the IMU are reported as quaternions (basically a short coding of the rotation between the IMU and the fixed laboratory system). Technically they are send to the Aduino (as a byte vector the fifoBuffer). On the Aduino the following steps happen:

1. The result of the FIFO Buffer is parsed and written in a Quaternion with components \(q=(q_w, q_x, q_y, q_z)\) this is done in `dmpGetQuaternion`

2. The vector of gravity is calculated in dmpGetGravity

3. From that vector (and the gravity) the yaw, pitch, and roll angles are calculated `dmpGetYawPitchRoll`

Code

 dmpMpu[num].dmpGetQuaternion(&q, fifoBuffer); 
 dmpMpu[num].dmpGetGravity(&gravity, &q);
 dmpMpu[num].dmpGetYawPitchRoll(ypr, &q, &gravity);

1.1 Getting the quaternion q

In the first line the quaternion send from the DSP is read from the fifoBuffer and parsed into the variable q. The quaternion q contains all information about a single IMU. This is done with the following code:

Code

uint8_t MPU6050::dmpGetQuaternion(int16_t *data, const uint8_t* packet) {
    // TODO: accommodate different arrangements of sent data (ONLY default supported now)
    if (packet == 0) packet = dmpPacketBuffer;
    data[0] = ((packet[0] << 8) | packet[1]);
    data[1] = ((packet[4] << 8) | packet[5]);
    data[2] = ((packet[8] << 8) | packet[9]);
    data[3] = ((packet[12] << 8) | packet[13]);
    return 0;
}

uint8_t MPU6050::dmpGetQuaternion(Quaternion *q, const uint8_t* packet) {
    // TODO: accommodate different arrangements of sent data (ONLY default supported now)
    int16_t qI[4];
    uint8_t status = dmpGetQuaternion(qI, packet);
    if (status == 0) {
        q -> w = (float)qI[0] / 16384.0f;
        q -> x = (float)qI[1] / 16384.0f;
        q -> y = (float)qI[2] / 16384.0f;
        q -> z = (float)qI[3] / 16384.0f;
        return 0;
    }
    return status; // int16 return value, indicates error if this line is reached
}

The yaw, pitch, roll information is calculated from the quaternion in two steps. First the vector pointing to the direction of gravity is calculated in dmpGetGravity

1.2 Calculation of the vector of gravity

This is the code from MPU6050_6Axis_MotionApps20.h

Code

        uint8_t MPU6050::dmpGetGravity(VectorFloat *v, Quaternion *q) {
          v -> x = 2 * (q -> x*q -> z - q -> w*q -> y); 
          v -> y = 2 * (q -> w*q -> x + q -> y*q -> z);
          v -> z = q -> w*q -> w - q -> x*q -> x - q -> y*q -> y + q -> z*q -> z;
          return 0;
        }

Mathematically speaking this code constructs the vector of gravity as follows:

\[ \begin{align} v_x &= 2 (q_x q_z - q_w q_y) \\ v_y &= 2 (q_w q_x + q_y q_z) \\ v_z &= q_w^2 - q_x^2 - q_y^2 + q_z^2 \end{align} \]

This translates into the following R code:

Code

dmpGetGravity = function(q){
  qw = q[1]
  qx = q[2]
  qy = q[3]
  qz = q[4]
  vx = 2 * (qx * qz - qw*qy)
  vy = 2 * (qw * qx + qy*qz)
  vz = qw^2 - qx^2 - qy^2 + qz^2
  return(c(vx,vy,vz))
}
q.vec = as.matrix(c(0.32,  0.30,  0.29, -0.85), ncol=1)
dmpGetGravity(q.vec)

[1] -0.6956 -0.3010  0.6508

1.2.1 What the code does

What is happening in the code? First, we note that quaternion \(q\), given back from the IMU transforms from the IMU coordinate system into the lab system. To make this clear, we write \(g = g_{L \leftarrow I}\) in the following. We are asking “How does the gravity” looks like on the IMU \(g_{I}\)? The gravity in the laboratory frame is given by \(g_{L}=(0,0,1)\). Note that, we could also define a different lab frame in which the gravity is e.q. given by \((0,1,0)\). From the Quaternion Algebra (see e.g. Note_on_Quaternion), we know that (L = Lab, I = IMU):

\[ q_{L} = q_{L \leftarrow I} \; q_{I} \; q_{L \leftarrow I}^{-1} \]

Where \(q_{\tt{L}}=(0,0,0,1)\) and \(q_{I}=(0,g_x, g_y, g_z)\) are pure quaternions, i.e. they take the vectors and set the real part \(w\) to 0. To solve for \(q_{IMU}\), we multiply with \(q^{-1}\) and \(q\) from left and right. Getting:

\[ q_{I} = q_{L \leftarrow I}^{-1} \; q_{L} \; q_{L \leftarrow I} = q_{I \leftarrow L} \; q_{L} \; q_{I \leftarrow L}^{-1} \]

We can verify this with the R-Code:

Code

q = as.quaternion(q.vec) 
qz = quaternion(Re = 0, k = 1)
qz

   [1]
Re   0
i    0
j    0
k    1

Code

q^-1 * qz * q

              Re
Re -2.220446e-16
i  -6.962963e-01
j  -3.013013e-01
k   6.514515e-01

Code

gravity = dmpGetGravity(q.vec)
gravity

[1] -0.6956 -0.3010  0.6508

1.3 Calculation of yaw, pitch, roll

The code in MPU6050_6Axis_MotionApps20.h used looks like follows:

Code

uint8_t MPU6050::dmpGetYawPitchRoll(float *data, Quaternion *q, VectorFloat *gravity) {
  // yaw: (about Z axis)
  data[0] = atan2(2*q -> x*q -> y - 2*q -> w*q -> z, 2*q -> w*q -> w + 2*q -> x*q -> x - 1);
  // pitch: (nose up/down, about Y axis)
  data[1] = atan(gravity -> x / sqrt(gravity -> y*gravity -> y + gravity -> z*gravity -> z));
  // roll: (tilt left/right, about X axis)
  data[2] = atan(gravity -> y / sqrt(gravity -> x*gravity -> x + gravity -> z*gravity -> z));
  return 0;
}

In math:

$$ \[\begin{align} {\tt yaw} &= {\tt atan2} (2 q_x q_y - 2 q_w q_z, 2 q_w^2 + 2 q_x^2 -1) \\ {\tt pitch} &= {\tt atan} (\frac{g_x}{\sqrt{g_y^2 + g_z ^2}}) \\ {\tt roll} &= {\tt atan} (\frac{g_y}{\sqrt{g_x^2 + g_z ^2}} ) \end{align}\] $$

This translate to the following R-Code.

Code

dmpGetYawPitchRoll = function(q, gravity){
  qw = q[1]
  qx = q[2]
  qy = q[3]
  qz = q[4]
  yaw = atan2(2*qx*qy - 2*qw*qz, 2*qw*qw+2*qx*qx-1)
  pitch = atan(gravity[1]/sqrt(gravity[2]^2+gravity[3]^2))
  roll = atan(gravity[2]/sqrt(gravity[1]^2+gravity[3]^2))
  return(c(yaw, pitch, roll))
}
as_arduino = dmpGetYawPitchRoll(q@x, gravity)
round(as_arduino,2)

[1]  2.28 -0.77 -0.31

The result from the Arduino is: (2.28, -0.77, -0.31). We can reproduce the results from the Arduino (see Comparison for more examples).

1.3.1 What the code does

For yaw it extracts the angle using quaternions. For pitch it uses the gravity calculated before (in the IMU space). Let’s start with the pitch and roll. From (https://ahrs.readthedocs.io/en/latest/filters/tilt.html we find (with \(a\) being the normalized gravity vector in the IMU space).

\[ \begin{align} {\tt pitch} &= \arctan2(-a_x, \sqrt{a_y^2 + a_z^2}) \\ {\tt roll} &= \arctan2(a_y, a_z) \end{align} \]

Pitch:

Code

#Pitch as As done on Aduino
atan(gravity[1] / sqrt(gravity[2]^2 + gravity[3]^2)) 

[1] -0.7702244

Code

#Pitch from 
a = gravity/sqrt(sum(gravity^2)) #Normalizing (we are almost normalized)
atan2(-a[1], sqrt(a[2]^2 + a[3]^2)) 

[1] 0.7702244

Except the sign, we got the same value as the code on the Arduino.

Roll:

Code

#Roll
atan(gravity[2] / sqrt(gravity[1]^2 + gravity[3]^2)) #As done in Arduino

[1] -0.3060571

Code

atan2(gravity[2], gravity[3])

[1] -0.4332065

For the roll, we get a different value compared to the Arduino.

2 Comparison with other methods

Usually the YPR is calculated differently not via the gravity first. In the following we compare different solutions, we found on the internet. The all use more or less the following

\[ \begin{align*} \text{roll} &= \text{atan2}(2 \cdot (w \cdot x + y \cdot z), 1 - 2 \cdot (x^2 + y^2)) \\ \text{pitch} &= \text{asin}(2 \cdot (w \cdot y - z \cdot x)) \\ \text{yaw} &= \text{atan2}(2 \cdot (w \cdot z + x \cdot y), 1 - 2 \cdot (y^2 + z^2)) \end{align*} \]

Code

  quart_to_ypr_as_arduino = function(q){
    gr = dmpGetGravity(q)
    return(dmpGetYawPitchRoll(q, gr))
  }
  #From poyu (value9250.py)
  #def quart_to_rpy(w, x, y, z):
  #  roll = math.atan2(2 * (w * x + y * z), 1 - 2 * (x * x + y * y))
  #  pitch = math.asin(2 * (w * y - x * z))
  #  yaw = math.atan2(2 * (w * z + x * y), 1 - 2 * (z * z + y * y))
  #  return yaw, pitch, roll
  quart_to_ypr = function(q){
    w = q[1]
    x = q[2]
    y = q[3]
    z = q[4]
    roll = atan2(2 * (w * x + y * z), 1 - 2 * (x * x + y * y))
    pitch = asin(2 * (w * y - x * z))
    yaw = atan2(2 * (w * z + x * y), 1 - 2 * (z * z + y * y))
    return(c(yaw,pitch,roll))
  }
  
  quart_to_ypr_as_arduino(as.numeric(q))

[1]  2.2792391 -0.7702244 -0.3060571

Code

  quart_to_ypr(as.numeric(q))

[1] -2.5986827  0.7692547 -0.4326218

2.1 Testing the code with special value

Note that the quaternion can be understood as a transformation of the IMU system into the fixed space system. Given a rotation about \(\theta\) and the rotational \(v_1, v_2, v_3\) the quaternion would be

\[ q=(\cos(\theta/2), \sin(\theta/2)v_1,\sin(\theta/2)v_2, \sin(\theta/2)v_3) \]

2.1.1 Single yaw

Let’s construct some special quaternions and see if the results are correct. Checking the yaw

Code

  q = c(0.30, 0, 0, 1.0) 
  q  = q / sqrt(sum(q^2))
  2*acos(q[1])

[1] 2.558679

Code

  rnames = c('yaw', 'pitch', 'roll')
  data.frame(
      arduino = quart_to_ypr_as_arduino(q),
      quart_to_ypr = quart_to_ypr(q),
      row.names = rnames 
    ) 

        arduino quart_to_ypr
yaw   -2.558679     2.558679
pitch  0.000000     0.000000
roll   0.000000     0.000000

2.1.2 Single pitch

Code

  q = c(0.10, 0, 1.0, 0.0) 
  q  = q / sqrt(sum(q^2))
  #The angle is 
  2*acos(q[1])

[1] 2.942255

Code

  #of
  pi - 2*acos(q[1])

[1] 0.1993373

Code

  data.frame(
      arduino = quart_to_ypr_as_arduino(q),
      quart_to_ypr = quart_to_ypr(q),
      row.names = rnames 
    )

         arduino quart_to_ypr
yaw    3.1415927    3.1415927
pitch -0.1993373    0.1993373
roll   0.0000000    3.1415927

There seems to be a numerical artifact.

2.1.3 Single roll

Let’s look at a single roll about the angle:

Code

  q = c(0.30, 1.0, 0, 0.0) 
  q  = q / sqrt(sum(q^2))
  2*acos(q[1])

[1] 2.558679

Code

  data.frame(
      arduino = quart_to_ypr_as_arduino(q),
      quart_to_ypr = quart_to_ypr(q),
      row.names = rnames 
    ) %>% 
  kableExtra::kable()

	arduino	quart_to_ypr
yaw	0.0000000	0.000000
pitch	0.0000000	0.000000
roll	0.5829136	2.558679

3 Comparison with Arduino for many values

This code shows that, we can reproduce the calculation done on the Ardunio for more examples.

Code

  #Loading
  training <- read.csv("../../data/value06.csv",header=TRUE)
  training = rename(training, IMU=X)
  
  training$IMU = as.factor(training$IMU)
  #nrow(training)
  training$t=rep(1:(1+nrow(training)/6), each=6)[1:nrow(training)]
  
  dat = training %>% filter(IMU != "0")
  dat_q = dat %>% select(starts_with('q'))

Code

  #YPR Calculation 
 ypr_calc = matrix(NA, ncol=3, nrow = nrow(dat_q))
  for (i in 1:nrow(dat_q)){
    gr = dmpGetGravity(t(dat_q[i,]))
    ypr_calc[i,] = dmpGetYawPitchRoll(t(dat_q[i,]), gr)
  }
  r2d = 360/(2*pi)

Code

  plot(r2d*ypr_calc[,1], r2d*dat$yaw, main='Calculated YAW (R vs Aduino) in degrees')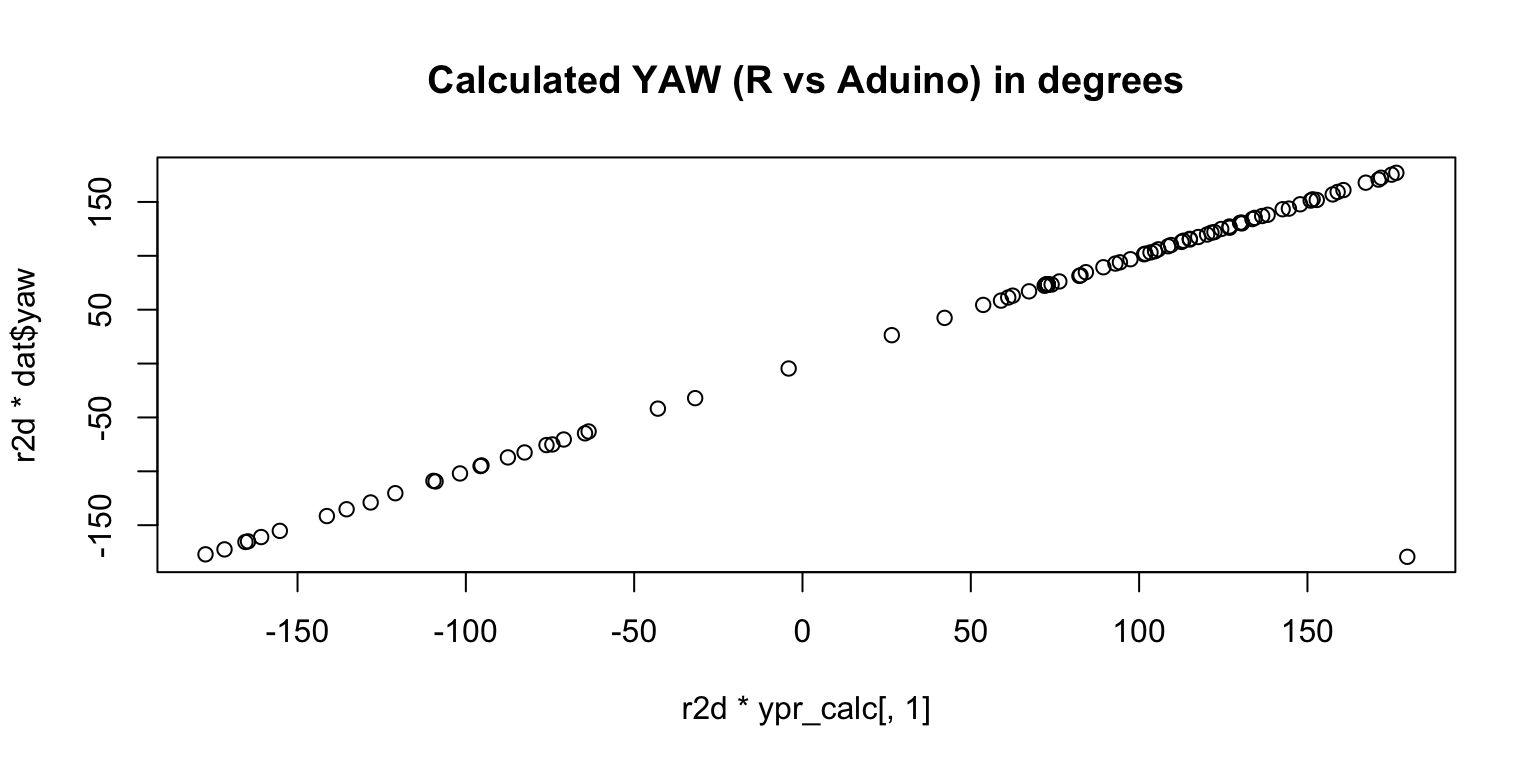

Code

  plot(r2d*ypr_calc[,2], r2d*dat$pitch, main='Calculated Pitch (R vs Aduino) in degress')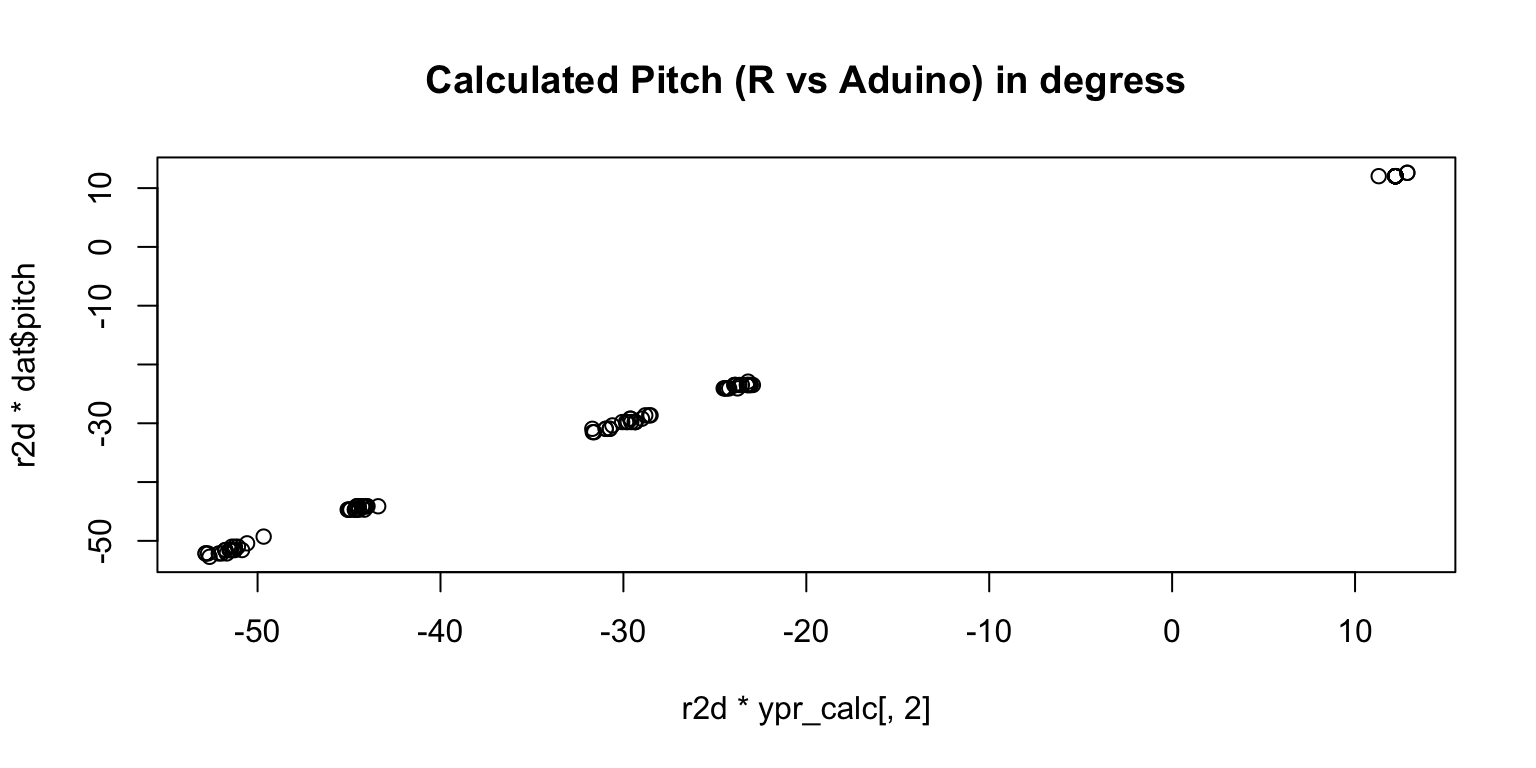

Code

  plot(r2d*ypr_calc[,3], r2d*dat$roll, main='Calculated Roll (R vs Aduino) in degrees')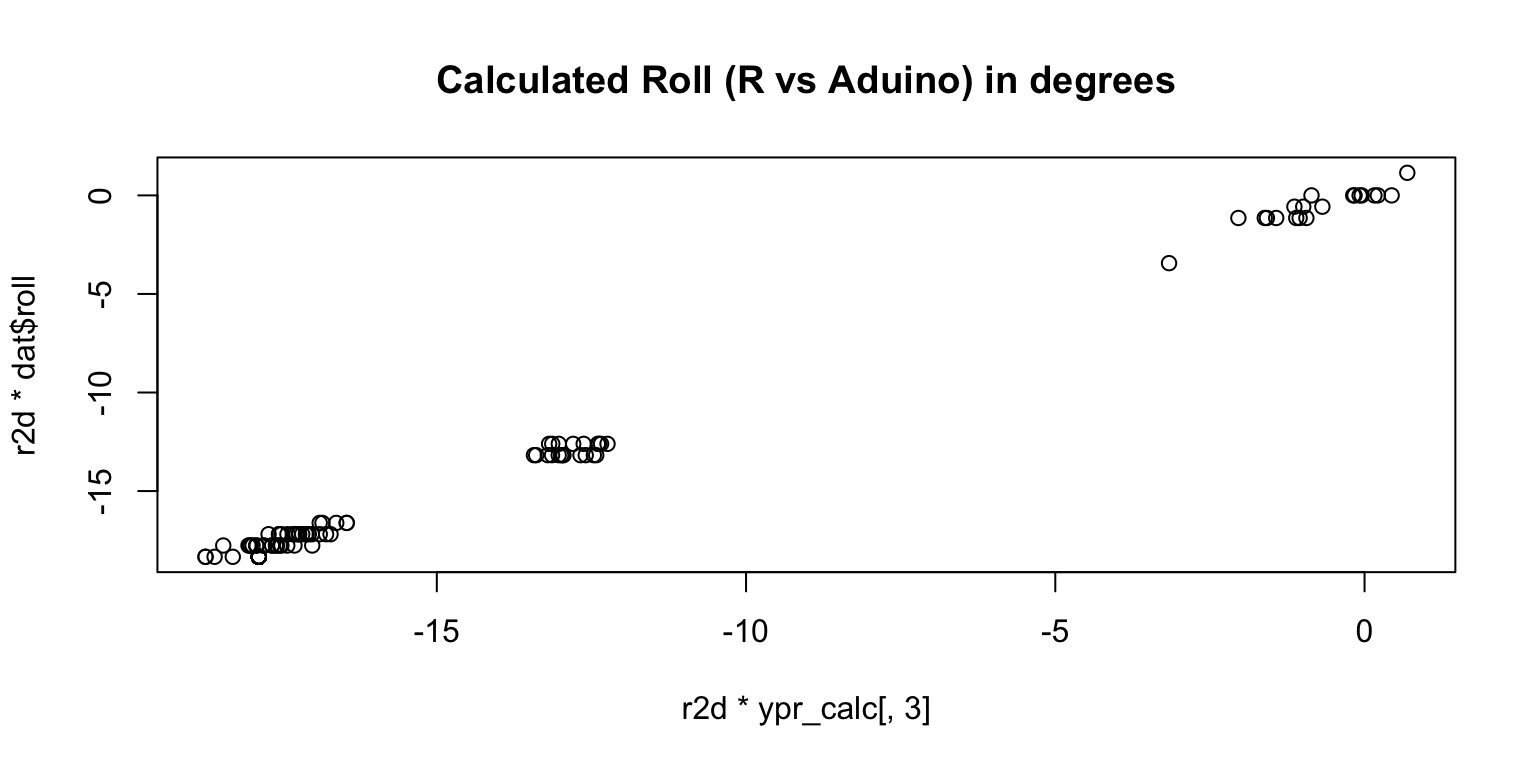

These plots show that, we can reproduce the Aduino values in R.